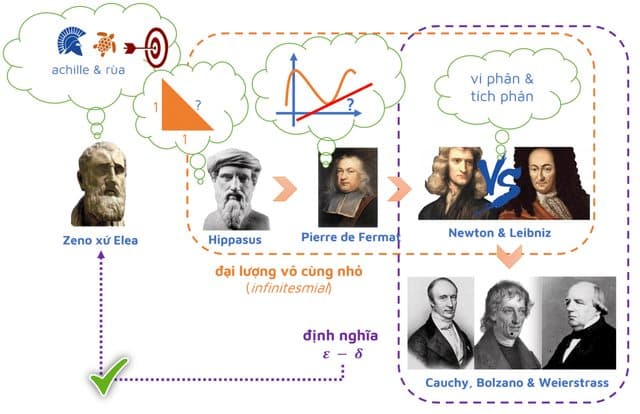
Đối với nhiều học sinh và giáo viên, một lớp học toán là nơi của sự chắc chắn tuyệt đối. Một cộng một bằng hai, sáu thì lớn hơn âm bốn và diện tích của một hình tam giác luôn bằng một nửa diện tích của một hình bình hành tương ứng. Xét theo quan điểm này, toán học là nơi mà luôn chứa đựng các câu trả lời không đúng thì sai, hoàn toàn không có sự mập mờ.
Vì thế có một chút bối rối khi ở lần đầu tiên tôi dạy một nhóm học sinh khi tôi cho các em xem một bộ bốn như hình dưới đây và hỏi “Cái nào khác với những cái còn lại nhất?“
Hình vẽ với câu hỏi “Cái nào khác với những cái còn lại nhất?“
Sau một hồi suy nghĩ, tôi yêu cầu một vài em học sinh đứng lên trả lời câu hỏi và giải thích cho câu trả lời của mình. Dưới đây là một số câu trả lời điển hình của các em.
- “Em chọn hình ở góc trên bên trái vì nó chỉ có 3 cạnh, các hình còn lại đều có 4 cạnh.”
- “Em chọn hình ở góc dưới bên trái vì nó không được tô màu trong khi các hình khác đều được tô màu.”
- “Em chọn hình ở góc trên bên phải vì khi xoay cùng chiều kim đồng hồ một góc 45 độ thì nó là hình duy nhất biến thành hình vuông đứng.”
- “Em chọn hình ở góc dưới bên phải vì nó có đáy là một cạnh trong khi các hình khác có đáy là một điểm.”
Các câu trả lời ở trên đều đúng khi nói về mối quan hệ của mỗi hình so với các hình còn lại. Vậy nên một câu hỏi mà tôi đặt ra lại có đến bốn đáp án khả dĩ? Nó không chắc chắn! Có sự mập mờ gì ở đây?!?
Tuy nhiên, sự mập mờ – một nơi hỗn độn những câu hỏi và câu trả lời không rõ tính đúng sai – lại là nơi rất thích hợp cho những ý tưởng toán học bắt đầu. Quay lại câu hỏi ở trên, điều cần quan tâm ở đây chính là điểm mà các em học sinh đang chú trọng vào dựa trên câu trả lời của các em. Nếu các em đếm số cạnh, các em đang làm hình học. Nếu các em chú ý đến phần tô màu, các em đang chú ý đến diện tích (phần được tô) và chu vi (đường viền bao quanh). Nếu các em nói về sự định hướng nghĩa là kỹ năng tưởng tượng không gian trong các em đang phát triển.
Thêm một câu hỏi tương tự khác, cũng là “Hình nào khác với hình còn lại nhất?“
Rất nhiều khám phá toán học khởi sinh chỉ việc thảo luận sự giống và khác nhau giữa các hình trên. Một câu hỏi được nhiều em học sinh phổ thông thảo luận chính là số góc hiện diện trong mỗi hình hay cụ thể hơn, số góc có trong hình trái tim?
Một luận điểm phổ biến chính là hình trái tim không có góc nào bởi vì góc chỉ được tạo thành khi hai đường thẳng cắt nhau, ở hình trái tim thì không có đường thẳng nào. Tuy nhiên cũng có một luận điểm khác nói rằng hình trái tim có tới hai góc bởi vì trên hình ấy có hai nơi gặp nhau của hai đường cong. Vậy suy cho cùng, luận điểm nào là chính xác phụ thuộc rất nhiều vào định nghĩa thế nào là một góc? Khi bạn đã có được định nghĩa chính xác của một góc, sự mập mờ sẽ bị xóa bỏ. Một định nghĩa chính xác của một góc cho phép bạn đo được góc ở đát hình trái tim dựa vào các phép tính vi tích phân. Tuy nhiên, không cần đao to búa lớn như thế, một học sinh nhỏ tuổi cũng có thể hình dung được dựa vào mắt mình rằng có một góc ở đáy hình trái tim và nó rất rất là nhỏ. Sự mập mờ tạo động cơ cho học sinh thảo luận sâu hơn, nhiều hơn về các ý tưởng toán học.
Một câu hỏi tạo ra sự mập mờ giống như hai câu hỏi ở trên không nhằm mục đích tạo ra sự tranh cãi hay rối rắm trong cách tiếp thu kiến thức của học sinh mà tập trung vào gợi ý, tạo một môi trường cởi mở cho học sinh thảo luận, tự bản thân tìm ra cốt lõi của vấn đề và định nghĩa thay vì chỉ tiếp thu một chiều từ các kiến thức của giáo viên đưa ra. Học sinh khi ấy sẽ được tiếp cận với các cái nhìn đa chiều của cùng một dạng kiến thức và nhớ lâu hơn, rõ ràng hơn. Rất nhiều nghiên cứu đã chỉ ra, bạn sẽ dễ dàng nhớ một điều gì đó hơn khi có sự sai lầm, mâu thuẫn, đối lập với điều ấy nảy sinh.
Tuy nhiên vận dụng phương pháp tạo sự mập mờ này không hề đơn giản, đòi hỏi khả năng lèo lái của người dạy học rất cao. Biết hỏi đúng câu, đúng lúc, gợi ý đúng chỗ và tạo hứng thú cho học trò.
Christopher Danielson. Dịch thoáng nghĩa bởi Math2IT, có chỉnh sửa và thêm một số ý.